We need some way of determining whether the diagnoses of SurveyMan's bugs is correct. It's always possible that a particular technique has a flaw in it, or that a test for a certain feature is not sensitive enough to detect the differences we would like it to detect. We have designed a simulator as a sanity check for our algorithms.

Simulator setup

The first step in our simulator setup is to generate gold-standard data; this is after all the reason for bothering with a simulator in the first place.

Consider the problem of bot detection. We will need to know the ground truth of who is a bot and who is not. Modeling bots explicitly is easy. We already do this in our static analysis. Modeling human respondents is more challenging.

We define a profile to be a collection of preferences over a survey. These preferences are the probabilities that an instance of a profile (i.e. a respondent) will choose a particular answer option for a question. For example, uniform adversaries will choose each answer option with equal probability.

In order to emulate human behavior, we allow the non-bot population of responses to be drawn from some number of clusters. A cluster is generated by randomly assigning a probabilities $$p_1$$ drawn from the interval $$(1/m_i, 1)$$ for each $$q_i$$. We say that a respondent belonging to one of these clusters has a preference for a particular answer, but may choose another answer due to factors we either cannot control or did not account for. These other preferences are assigned uniform probability : $$\frac{1-p_i}{m-1}$$. Sometimes a preference will be very strong (e.g. assigned a probability > 0.8). Sometimes the preference will only be slight, in which case it will be close to $$1/m_i$$.

We can then inject biases into the generated responses and test our bias detection algorithms, testing the robustness of our techniques by varying the impact of bad actors on our results.

Correlation

Any measure of correlation between questions in the survey must consider what's called the "level of measurement" of each question. Levels of measurement determine the statistical tools we can use to analyze the data. There are four levels of measurement in total:

1. Nominal Data that fall into categories that have no order are said to be nominal. Generally this will correspond to radio button questions such as "What is your gender." This data will be represented by a categorical variable and permutation tests will have to be used to analyze any correlations. Tests on nominal data are sensitive to sparsity; since they are not continuous, we cannot use interpolation to make inferences.
2. Ordinal Ordered questions fall into this category. This is probably the most common type of survey question. Surveys that ask users about their preferences or to provide rankings for data are using ordinal data. The more common and powerful statistical significance and correlation tests begin at this level.
3. Interval Where ordinal questions required the ability to rank, interval questions require there to be meaningful distances between answer options. Likert scale questions are an attempt to capture interval questions (although they are often analyzed using ordinal tests, since their measurement is imperfect). Interval questions attempt to capture the magnitude of difference between ranked answers.
4. Ratio Ratio questions are "true" numeric questions - that is, individual answers have meaningful magnitude because there is a known underlying zero grounding the measurement. Weight, date of birth, and income are all ratio questions. These questions permit the most powerful statistical tests because data can be interpolated.

SurveyMan uses correlation in two ways. The CORRELATED can be used to flag sets of questions that the survey designer expects to have statistical correlation. Flagged questions can be used to validate or reject hypotheses and to help detect bad actors. Alternatively, if a question that is not marked as correlated is found to have statistically significant correlation, then we flag this question. Questions are compared on a pair-wise basis. This information can be used in a variety of ways :

• The survey designer could decide to remove one or more of the correlated questions, if their predictive power is strong enough to infer responses from the remaining questions. It is ultimately the responsibility of the survey designer to use good judgement and domain knowledge when deciding to remove questions; note that because we only check pair-wise correlation, we cannot capture the impact of groups on a particular outcome. We do not model interactions between variables.
• The survey designer could use discovered correlations to assist in identification of cohorts or bad actors by updating the entries in the CORRELATED column appropriately.

We only support automated correlation analysis between exclusive (radio button) questions. These questions may be ordered or unordered.

For two questions such that at least one of them is unordered, we return the $$\chi^2$$ statistic, its p-value, and compute Cramer's $$V$$ to determine correlation. We also use Cramer's $$V$$ when comparing a nominal and an ordinal question. Ordinal questions are compared using Spearman's $$\rho$$. Since in practice we rarely have sufficient data to return confidence intervals on such point estimates, we simply flag the pair and leave the interpretation of the values up to the survey designer.

For non-exclusive (checkbox) ordered questions, we would need a meaningful metric to understand what the relationship between subsets of checkboxes are. For example, in a question of four answer options A, B, C, and D, we would need to know how to compare the answers {A,B}, {B,C}, and {A,C}. If their values are additive and we let their weights correspond to their indices, how far apart are the choices {A,B} and {C}? Any analysis would have to be domain-specific and thus falls outside the scope of SurveyMan.

For non-exclusive (checkbox) unordered questions, we also run into trouble. We don't have to worry about specialized distance functions, but we do have to worry about the fact that our categories are not exclusive. That is, we can no longer use a categorical random variable to represent the question, since a single respondent may belong to multiple categories. This violates the conditions of all known tests. We could use subsets as our events instead and analyze them as we do with exclusive data. However, the contingency table for a question $$q_i$$ having $$m$$ options will have $$2^m - 1$$ as one of its dimensions. While Cramer's $$V$$ reduces the impact of the degrees of freedom on the $$\chi^2$$ test, we still have the problem of sparsity in the table's cells. We observed in simulation that, as sparsity increased, the range of errors increased. While we would still sometimes see the injected correlated questions show up, we also saw many more cases of a question being classified as having a correlation coefficient close to 0 when compared against itself. The misclassification wasn't too bad for three checkbox options, but it was unacceptable at 4. As a result, we do not support correlation on checkbox questions.

If users want to do correlation on checkbox questions anyway, they can enumerate the subsets and display these as exclusive questions. It's true that the very problem we try to avoid with checkbox questions could still be a problem with radio button questions. However, it's unusual in practice to have a large number of nominal choices. We could compute the required number of random respondents needed to have at least 5 entries in each cell of the contingency table and only analyze correlation if this condition is met. This is something to consider for future SurveyMan releases and requires further investigation.

Where does the runtime fit in?

A SurveyMan workflow looks something like this :

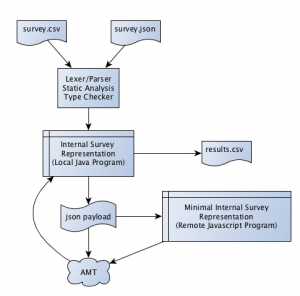
We currently only support csv input; the design of the csv language is such that a human could reasonably write a survey in it. Molly is currently working on a Python library that will streamline some of the more advanced features of SurveyMan and Python proficient users to design surveys in Python and output a JSON equivalent to a csv survey.

The main SurveyMan program is written in Java. It handles all of the static checks on the input and loads the survey into an internal representation. When it is time to send the program to a crowdsourcing platform, the Java program produces a minimal JSON representation of the survey and sends this wrapped in HTML. When the crowd platform is Mechanical Turk, the HTML is sent inside an XML payload and handled by AMT. When the platform is a local server, it just sends the HTML. We can support any crowdsourcing platform that allows us to send arbitrary HTML.

We send the minimal JSON representation for two reasons. The first is that for AMT, we have a maximum payload allowed. The second reason is because not all of the survey data is useful to the runtime. We need sufficient information to determine how to display the survey to the user. We don't do any analysis on the crowdsourcing platform, so we don't need to send over information like the CORRELATED column or any user-provided columns. We do allow survey designers to add custom Javascript to their survey, which can be used to perform computations and return the results of those computations.

Input

The input to the SurveyMan program is a survey csv. This csv is parsed and loaded into an internal representation, which is then translated into a JSON payload. The resulting JSON representation of the survey is sent to the crowdsourcing platform. This survey JSON is then interpreted by a Javascript program that controls flow through the survey and how individual questions are displayed.

The Finite State Machine

SurveyMan surveys are interpreted in Javascript on a finite state machine that controls the underlying evaluation and display.

There are two layers to the survey interpreter. The first handles survey logic; it essentially runs in a loop, proffering questions and consuming responses. The second layer handles display information, updating the HTML in response to certain events.

User's view of the FSM

A respondent navigates to the webpage displaying the survey. For AMT, we show a consent form in the HIT preview. When an individual accepts a HIT, they begin a survey. The consent form mechanism is not currently implemented in the local server.

The user then sees the first question* and the answer options. When they select some answer (or type in a text box), the next button and a "Submit Early" button appear. If the question is instructional and is not the final question in the survey, only the next button appears. When the respondent reaches the final question, only a

Each user sees a different ordering of questions. However, a single user's questions are presented in the same order; the random number generator is seeded with the user's session or "assignment" id. In AMT, this means that if the user navigates away from the page and returns to the HIT, the question order will be the same upon second viewing.

Only one question is displayed at a time. This design decision is not purely aesthetic; it helps us measure breakoff.

Underlying machinery

In addition to the functions that implement the state machine, there are three other underlying data structures:

1. Block Stack : Since our path through the survey is determined by branching over blocks, and since we may only branch forward, we keep the top-level blocks on a stack.
2. Question Stack : Once we know which block we're to execute, we can fetch the appropriate questions for that block.
3. Branch Reference Cell : The branch target is stored here, since we defer executing any branching at least until all of the questions in the block have been seen.

The SurveyMan interpreter is initialized as follows : the survey JSON is parsed into an internal survey representation and then randomized using a seeded random number generator. This randomization preserves necessary invariants (e.g. the partial order over blocks). We then push the top level blocks onto the block stack. Then we pop off the first block and initialize the question stack using getAllQuestions.

The interpreter's execution runs as follows :

procedure run
begin
  while blockStack is not empty
  do
    question <- getNextQuestion()
    display question and answer options
    answer <- user-provided answer
    store answer
    if the question is a branch question
    then
      branchRef <- answer's branch destination
    fi
    if user selects submit
    then
      return stored answers
    fi
  done
  return stored answers
end


Answers are stored in the HTML forms in the usual way. We have three main divs in the HTML : one for the displayed question, one for the displayed answers, and one for response input data. The response input elements are kept in a hidden div below the answer display div. Each new response is inserted above the previous one, emulating a stack.

The function getNextQuestion handles control flow and is the primary point of interaction with the FSM:

function getNextQuestion
  output : question
begin
  if questionStack is empty
    if branchRef is set
    then
      while true
      do
        nextBlock <- peek(blockStack)
        if nextBlock = branchRef
        then
          questionStack <- getAllQuestions(pop(blockStack))
          unset branchRef
          break
        else if nextBlock is a floating block
        then
          questionStack <- getAllQuestions(pop(blockStack))
          break
        else
          pop(blockStack)
        fi
      done
    else
      questionStack <- getAllQuestions(pop(blockStack))
  fi
  return pop(questionStack)
end


Determinism in the runtime

There are two main sources of nondeterminism in SurveyMan. The first is our random number generator; the second is human behavior.

We had previously generated a new static HTML version of the survey for each respondent. Each question was contained in its own div and branch destinations pointed to these divs. None of the blocking structure was visible to the user. The Javascript was minimal; if the question was a branch, it would hide the current question and display the the div with the appropriate id. If the question did not have branching, it would navigate the DOM and just display the next div.

This prior approach lead to a technical issue that proved to be a nice metaphor for the underlying system. The problem was that, since we had to send over unique HTML for every desired respondent, we ended up with many HITs posted on AMT. AMT groups together HITs that have similar parameters and facilitates workers' acceptance of consecutive HITs in groups. Having many HITs not only attracted bad actors, but it also annoyed honest respondents, who did not always realize that they were not supposed to answer all of the HITs.

While each respondent sees a different version of the survey, the underlying survey is essentially "the same." It made more sense to move the survey logic into the Javascript and post a single HIT. It was also cleaner to group together user behavior with survey execution, rather than flattening the survey and adding an extra (albeit simpler) evaluator that primarily responded to user nondeterminism.

What's key about these two approaches is that the two types of nondeterminism are quite different from each other. Randomization gives us predictable behavior in the limit and, depending upon the task may not even have an impact on the computation. Randomization does not occur in response to user behavior and can be done before executing anything. Once we know which block to execute, the total set of questions is almost deterministic. That is, rather than having to account for nondeterminism and uncertainty at every step in the evaluation, we only have to handle it at known junctures. So long as we can prove that the set of surveys produced at each junction are equivalent, we know that the evaluation is sound.

* The respondent may also see a breakoff notice first. This is just a page stating that they may submit results at any time and that they will be paid bonuses commensurate on the number and quality of questions answered. It can be turned off.

We are now calling "randomizable" blocks "floating" blocks. Kudos to Emery for the increased clarity.

I just thought I'd post a diagram I made of valid orderings for questions and blocks. We can think about how hierarchical blocks allow the user to impose an ordering on the question and to introduce a guarantee about the distance between two questions. When we permit blocks to be randomizable, we relax the former.

The key invariant we wish to preserve throughout the survey is that an individual's answers are the same, no matter which version of the survey they see. That is, if the same respondent were to take the survey twice, beginning to end, the total number of questions seen and answers given would remain the same. We'll see in this post how this invariant influences enumerating and computing metrics on paths. In a later post, we'll see how this invariant leads us to analyze survey "bugs."

We use paths through the survey to aid in the debugging process and to automate some parameters to the crowdsourcing backend. Let's take a moment to look at how some of the design choices we've made impact possible paths through the survey:

Top-level blocks

At the top level, a survey is composed of blocks. If there are no blocks (i.e. the survey is completely flat), we can say that all questions belong to a single block.

Top-level blocks have the following branch requirements:

1. There is only one "true" branch question per block.
2. Branch question destinations must all be top-level blocks.

If there is a branch question, it may appear in any position, subject to any blocking constraints. The branching action isn't evaluated until every question that we plan to execute in the block is executed.

Randomizable blocks

Top-level randomizable blocks are not allowed to have branch questions. They also cannot be branch destinations. Permitting branching to or from randomizable blocks could cause us to have a loop in the program. For example, if block 3 branches to some randomizable block we'll call X, and X happens to appear before block 1, we have a problem, since we will have already executed X. Similarly, if we branch from X to 3 and X appears as the last block in a survey, we will also have a loop.

In addition to violating our DAG guarantee, branching to or from randomizable blocks could cause nondeterminism in the number of questions asked. If block 3 branches to X, but X is the last block in the survey for one person, but immediately follows 3 for another, we will be allowing randomness to have an influence on the answer set.

Note that if we are using branching for sampling, the above doesn't apply.

On the other hand, randomizable subblocks may be a branch source. If their branch destination is ALL, we have no conflicts, since we will choose the next (randomly determined) sequential question as usual. If their branch paradigm is ONE, then their branch question becomes the one branching question for the topmost enclosing block. This is exactly the same as for non-randomizable subblocks.

Enumerating paths

We stated at the beginning of this post that answer sets should be invariant for the version of the survey seen. In the previous post, we described how path data can be used for static analysis.

When we view a path through the survey as the series of questions seen and answered, the computation of all such paths is intractable. Consider a short survey we recently ran that had 16 top-level randomizable blocks, each having four variants and no branching. We have 16! total block orderings. Then, since we choose from four different questions, we end up with $$2^{16!}$$ unique paths.

Fortunately, the computations we mentioned in the static analysis post do not require knowing the contents of the path. They only require that we know the size of the path. Since we have required that every appropriate question in a top level block be executed, we can treat top level blocks as nodes in the possible survey DAG. The weight of these nodes (i.e. the size of the block) can be computed statically. Then we only need to consider the branching between these top level blocks.