What code review should actually be like (and related problems with AI)
John sent me a blog post about a month ago that was already old when he saw it. I thought I'd post about it because I see a larger issue with how (lay)people understand AI in it.
The post is here. It contains some musings about how to measure sortedness of a list.
I'm going to walk through the problems I see with this post:
How do you measure the "sortedness" of a list? There are several ways. In the literature this measure is called the "distance to monotonicity" or the "measure of disorder" depending on who you read. It is still an active area of research when items are presented to the algorithm one at a time. In this article, I consider the simpler case where you can look at all of the items at once
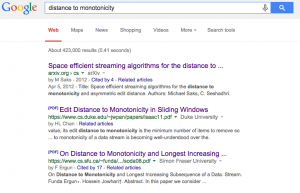
What literature? Links? My CLRS algorithms book is currently on loan to a labmate, so I can't search its index, but I'm pretty sure the average computer science student would be introduced to it through that route. A quick google search of "distance to monotonicity" gives the following results in Google:
A quick review of the links verifies what the author says (note that I didn't get anything meaningful for "measure of disorder," so links there would have been good).
The next paragraph mention's Kendall's distance. I thought I'd never heard of it, so I searched for it. It appears that the author was basically talking about Kendall's tau, which I have heard of/used. Kendall's tau is used widely for inter-annotator agreement and relevance judgements. These measures are widely used in linguistics, NLP, information retrieval and extraction, etc. Its application to sorting lists isn't quite right -- tau was designed for ordinal data, where the distance between ranks is not something we can really quantify. Consider its use in search: it's clear that the Wikipedia page when searching with the query "Kendall's tau" should be more relevant than a domain-specific paper that uses Kendall's tau, but it's not clear whether there is a meaningful measure of how much more relevant Wikipedia is. Furthermore, there is no notion of inherent distance between the Wikipedia hit and the paper. If these are the only two documents on the web, then Wikipedia should be ranked first and the paper should be ranked second. However, if we introduce a document from a statistics class taught at University of X, it should probably be ranked second, and the paper third. Conversely, if we're sorting a list of integers, we know that 2 will always following 1 and that we cannot introduce any numbers that ought to be ranked between 1 and 2 without breaking out of the set of integers. This brings us to the next problem with the post.
The problem states it is about the sortedness of lists, but what it's really about is the sortedness of compact lists. I think this is what the author is trying to say when he critiques edit distance and longest increasing subsequence: "A drawback of this method is its large granularity. For a list of ten elements, the measure can only take the distinct values 0 through 9." I don't recall LIS having a problem with duplicates, and I also don't remember it requiring compactness. In fact, I'm pretty sure there is a O(n log n) algorithm for any sequences of items that has a comparator relation defined on it. Conversely, the metric the author proposes does not have these properties. Let's take a closer look:
Here, I propose another measure for sortedness. The procedure is to sum the difference between the position of each element in the sorted list, x, and where it ends up in the unsorted list, f(x). We divide by the square of the length of the list and multiply by two, because this gives us a nice number between 0 and 1. Subtracting from 1 makes it range from 0, for completely unsorted, to 1, for completely sorted.
$$1 - \frac{2}{N^2}\sum_{i=1}^N \lvert f(x_i) - x_i \rvert $$
The $$\lvert f(x_i) - f(x_1) \rvert$$ part looks okay (for now -- it' really not, but I'll get to that below). The distance between two indices (where the item is and where it should be) is in one dimension, and direction doesn't matter. Presumably $$N$$ is the size of the list. The sum of all these distances would be the total distance moved if we were copying to another location. Why isn't this the distance if we perform the operations in place? Because we are going to need to put the displaced value somewhere. Consider the following two lists: [2,1,4,3,5,6] and [6,2,3,4,5,1]. Using the above formula, we see that the first is considered more sorted than the second. However, the first requires more swaps to sort than the second. One could argue that we are simply not interested in swaps as a cost unit in this context. However, in a post about sortedness, this seems like a foolish argument to make (and if the author wanted to make the argument in terms of entropy and argue that the distance of the swap matters more, then he should have focused on this instead).
In any case, $$\lvert f(x_i) - f(x_1) \rvert$$ makes some sense in a particular context. The sum also makes sense in a particular context (copying). However, it is not clear at all why we are normalizing by $$\frac{2}{N^2}$$. When computing the cost of comparison operations that are not symmetric, it's common to use a double-nested loop to compare each item with each of the others. If we were to compare every item we, we would have $$N^2$$ operations. If comparing against oneself is a waste of time, then every item only compares against every other item, and we have $$N(N-1)$$ operations. If we only need to compare in one direction (e.g., if we use a symmetric operation, like absolute value), then we can cut these comparisons in half: $$\frac{N^2 - N}{2}$$. I could use see someone using the total number of operations as a normalizing factor. Furthermore, someone could argue that the exact number of comparisons are not needed, only an upper bound, so $$\frac{N^2}{2}$$ is good enough. This is where I believe the normalizing factor of $$\frac{2}{N^2}$$ comes from. I do not however think it is justified, since it is still based on the number of comparison and there are better metrics out there.
Finally, we subtract this quantity from one, since lower is better (but we humans like to think more is better).
Now for an analysis of the code.
First of all, the code does not actually match the formula. $$x_i$$ in the formula is the target location of the item. However, the $$x_i$$ in the code (see where enumerate is called: $$x_i$$ is called element) is the value of the item in the list itself. This means that the author is expecting us to only be sorting numbers. Furthermore, subtracting the value from the index in which it appears confirms my suspicion that this approach only works for a very small subset of lists. In fact, the code restricts the lists that this technique sorts even further by assuming that they start at 1. That is, a sorted list of [2,3,4,5,6] cannot have a score of 1!
My second problem with this approach is that the solution to the problem is encoded directly in the fitness function! You could just copy the list out to the appropriate order. The whole point of search-based AI techniques like GAs is that you "know it when you see it," but you cannot generate the appropriate solution yourself (or doing so would be costly).
The Meta Part
So first of all, why am I picking on this guy? I am a PhD student in computer science and he is putting himself out there thinking about these problems. My worry is that people's eyes tend to glaze over when it comes to math. I admit, when I first saw this blog post, I didn't read carefully and just assumed it was a neat insight. I think it's important to play around with these ideas, but it's also important to not accept what someone else has reasoned about without questioning. The blog post begins with a summary of the problem and even notes that a particular formulation of the problem is an active area of research. I worry this has the effect of setting up the reader to believe the author is an authority on the subject.
As for the parenthetical part of the title of my post, this guy's post doesn't discuss AI at all, but it does present a short implementation of a genetic algorithm for sorting a list using the metric the author defines. The reason why I'm framing this post as a problem with AI is because I think this post illuminates major mistakes people when applying AI.
Now, I don't meant to take the author of the post to task. It's just a one-off blog post that was probably fun to write. However, I do think it's illustrative of how techniques from AI and statistics are presented as if they can be used off the shelf as a black box, when in fact they are only appropriate for specific problems. Certainly there are things we could be doing to ameliorate this mismatch. The fact that people are "doing it wrong" is not entirely their fault and we should be doing more to make these techniques "safer." We did this in programming languages, with static typing and static analysis tools. It's time to start doing it in AI.